Der Minimax-Algorithmus

Allgemeines:

Ein Brettspiel, welches von zwei Personen gespielt wird, kann auf eine einfache Weise als Baum dargestellt werden.
Dabei kennzeichnet jedes Blatt eine Spielkonfiguration, d.h. auch innere Blätter, oftmals auch als Knoten bezeichnet, stellen eine Stellung der Steine auf dem Spielfeld dar.
Weiterhin wird festgelegt, daß eine Verzweigung dieses Baumes, einen Übergang von einer Spielstellung zu einer anderen, welche durch einen Zug erreicht werden kann, kennzeichnet.
Die Schichten des Baumes, p, ist die Anzahl der Stufen des Baumes, inclusive der Wurzelschicht. Wenn also die Tiefe des Baumes d ist, so ergibt sich p zu p=d+1.

Da es nun nicht möglich ist den Baum vom Anfang an nach alles möglichen Spielkombinationen abzusuchen, muß man sich etwas besseres einfallen lassen (bei einem Schachspiel mit 100 Zügen und 16 Figuren würde eine Anzahl von Möglichkeiten im Bereich 10exp(120) herauskommen).
Also beschränkt man sich auf eine gewisse Anzahl von Zügen, welche im Vorraus berechnet werden. Davon wählt man dann den Zug welcher in die Richtung der günstigsten Spielstellung führt. Leider gibt es aber keine universelle Prozedur zur Einschätzung von Spielstellungen. Daher muß man sich eine geeignete Möglichkeit ausdenken solch eine Spielstellung über eine Punktzahl zu characterisieren.
Ein weiteres Problem ist natürlich, daß der Aufwand nicht wesentlich sinkt wenn nun jede mögliche Spielstellung welche innerhalb der vorauszuberechnenden Züge liegt ausgewertet wird. Es ist also eine weitere Vereinfachung erforderlich.

Der Minimax-Algorithmus:

Anstatt nun alle Spielstellungen zu bewerten kann man sich überlegen, daß man immer die beste Stellung erreichen will (per Konverntion die Spielstellung mit der höchsten Punktzahl). Andererseits wird der Gegenspieler aber das gleiche versuchen. Also ordnet man einem Spieler eine maximale Punktzahl zu und dem anderen eine minimale.

Man nennt den Spieler, welcher die maximalen Punkte erhofft, auch den "Maximizer" und den Gegenspieler den "Minimizer".

Da die Spieler nun abwechselnd eine Spielfigur ziehen, ist immer ein Spieler auf einer bestimmten Baumebene am Zug. Daher kann man diese Ebenen auch danach benennen, welcher Spieler dort am Zug ist. Man nennt diese Ebenen dann Maximizing und Minimizing level.

Daraus kann man nun folgenden Baum ableiten:

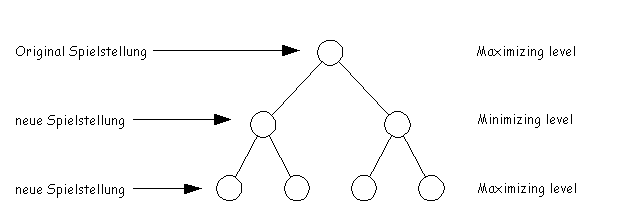
Der Maximizer hofft also, daß er aus den unter sich liegenden Schichten das Maximum herausholen kann und der Minimizer will das Minimum herausholen. Da aber nur die Endstellungen bewertet werden, beginnt man von unten und arbeitet sich dann nach oben durch (das entspricht einem Baumdurchlauf in Postorder).

Dazu ein Beispiel:

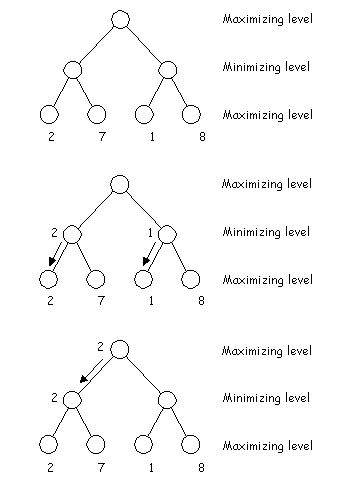
Der Maximizer möchte möglichst die Situation mit der 8 erreichen. Er würde damit dem Minimizer aber die Chance auf eine 1 eröffnen. Da er aber immer mit dem besten Zug des Minimizers rechnen muß wählt er lieber die 2.
Oder man betrachtet es immer aus der Sicht des Spielers, welcher gerade am Zug ist, wobei man von unten beginnt. Danach wäre zuerst der Minimizer dran, welcher den Zug wählt, welcher die wenigsten Punkte bringt (daher auch Minimizer). Er wählt also im linken Teilbaum die 2 und im rechten die 1 und übergibt das Ergebnis an den Maximizer, welcher von den möglichen Werten natürlich die 2 wählt (das Maximum).

Der formale Algorithmus sieht also so aus:

 Man kann das auch an dem obigen Beispiel Prüfen:

daraus folgt dann, daß der nächsten Zug des Maximizers nach links führen wird.

Wenn man sich aber nun vorstellt, daß alle Möglichkeiten getestet werden müssen, kann es bei einer Tiefe von z.B. 5 Stufen und einem Verzweigungsgrad von 7 und mehr, doch schon recht aufwendig werden.
Deshalb führt man eine Verbesserung des Algorithmusses ein, da man oftmals schon frühzeitig feststellen kann, daß ein bestimmter Weg so schlecht ist, daß man gar nicht mehr wissen möchte wie schlecht er ist.

Das Alpha-Beta Prinzip:

Das Prinzip wird am besten an einem Beispiel deutlich:

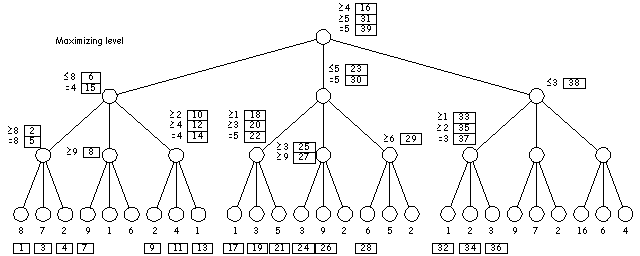
Was passiert nun ?

  1. (Schritt 1-2) Man geht den linken Ast bis zum Ende herunter und findet eine 8, was heißt, das der Maximizer in diesem Ast eine maximale Punktzahl von 8 erreichen kann (dies ist durch Schritt 2 gekennzeichnet).
  2. (Schritt 3-5) Der Maximizer testet nun ob er noch eine höhere Punktzahl durch die zwei anderen Züge erreichen kann, findet aber nur die 2 und die 7. D.h. er kann in diesem Ast maximal eine 8 erreichen (dies ist durch Schritt 5 gekennzeichnet).
  3. (Schritt 6) Da nun ein Ast bekannt ist kann der Minimizer, eine level darüber, auf eine Punktzahl <= 8 hoffen.
  4. (Schritt 7-8) Damit der Minimizer sein entgültiges Ergebnis erhält, müssen seine beiden anderen möglichen Züge noch getestet werden. Der erste Zug führt zu einer Position, in welcher der Maximizer maximal eine 9 erreichen kann (da dies größer als 8 ist, brauchen die beiden anderen erreichbaren Ergebnisse des Maximizers nicht weiter untersucht werden - hier greift das Prinzip, daß man gar nicht wissen möchte wie schlecht es noch werden kann). Daraus folgt, daß keine Änderung in der Minimizer level auftritt. Das beste Ergebnis für ihn ist immer noch <= 8.
  5. (Schritt 9-14) Nun wird die letzte Möglichkeit für den Minimizer untersucht, er schaut also was der Maximizer dort maximal erreichen kann. Das erreichbare Maximum in diesem Teilbaum lautet 4.
  6. (Schritt 15) Der Minimizer wählt also den rechten Ast, da dort der Maximizer sein kleinstes Ergebnis (die 4), welches kleiner ist als das bisherige Minimum, erreichen kann.
  7. (Schritt 16) Nun kann diese 4 an die top level übergeben werden. Der Maximizer sieht dort, daß der linke Ast zu einem maximalen Ergebnis von 4 führt. Er untersucht nun die beiden anderen Möglichkeiten um zu schauen ob nicht doch eine höhere Punktzehl zu erreichen ist.
  8. (Schritt 17-22) Mit der Annahme, daß der Minimizer immer den Zug macht, welcher zum geringsten Ergebnis führt, untersucht nun der Maximizer die Möglichkeiten und stellt fest, daß er im mittleren Ast und dann im linken eine Punktzahl von 5 erreichen kann.
  9. (Schritt 23) Der Minimizer stellt fest, daß der Maximizer im linken Ast eine 5 erreichen kann und hofft auf ein Ergebnis welches kleiner ist.
  10. (Schritt 24-27) Die Untersuchungen gehen weiter im mittleren Ast des Minimizers, aus welchem der Maximizer eine 9 holen könnte, was aber der Minimizer nicht akzeptieren würde (da er ein Ergebnis <= 5 erwartet), so daß dort die Untersuchungen beendet werden können.
  11. (Schritt 28-29) Wenn man nun in den rechten Ast des Minimizers schaut erkennt man schnell, daß dort der Maximizer die Chance auf eine höhere Punktzahl als 5 hat. Also kann man auch dort mit der Untersuchung aufhören.
  12. (Schritt 30) Da der Minimizer nun alle Möglichkeiten untersucht hat muß er feststellen, daß minimal eine 5 zu erreichen ist.
  13. (Schritt 31) An der Wurzel stellt der Maximizer nun fest, daß im mittleren Ast eine Punktzahl von 5 zu erreichen ist, d.h. er hofft nun im linken Ast auf eine Punktzahl >=5.
  14. (Schritt 32-37) Nun muß der rechte Ast des Maximizers noch untersucht werden. Also untersucht der Minimizer in der level darunter erst einmal den linken Teilbaum, und stellt fest, daß er dort eine Punktzahl von 3 erreichen kann.
  15. (Schritt 38) Der Minimizer kann also auf eine Punktzahl <= 3 hoffen.
  16. (Schritt 39) Mit dem Wissen, daß der Minimizer eine Punktzahl <=3 im rechten Teilbaum erreichen kann, weiß der Maximizer in der top level, daß es im rechten Teilbaum keine Chance mehr gibt eine Punktzahl >= 5 zu erreichen.
    Nach all dem weiß er also, daß er, wenn er dem mittleren Ast folgt, mindestens eine Punktzahl von 5 erreicht.

Das besondere an dieser Methode ist also, daß nicht alle Möglichkeiten einer vorgegebenen Tiefe untersucht werden brauchen. In obigen Beispiel brauchen z.B. nur 16 Stellungen, statt 27, bewertet werden.

Programmiertechnisch löst man das Problem mit den Grenzwerten so, daß man die ganze Untersuchung rekursiv gestaltet. Dafür schreibt man sich eine Prozedur mit den beiden Parametern alpha und beta, welche die nötigen Untersuchungen aufzeichnen. Diese ALPHA-BETA-Prozedur startet nun an der Wurzel mit einem alpha-Wert von -Unendlich und einem beta-Wert von +Unendlich. Danach ruft sich die Prozedur rekursiv wieder auf, mit einem kleineren Bereich zwischen alpha und beta:

Um die Minimax-Suche mit der ALPHA-BETA-Prozedur auszuführen, tut man folgendes:

Bei Fragen, Unklarheiten oder anderen Problemen bitte wenden an: steko@kbs.uni-hannover.de